提要：年龄-时期-世代模型是研究社会变迁的重要工具，但年龄、时期和世代之间存在完全共线性，使得求解该模型面临严峻的挑战。本文回顾了现有关于该模型的各种求解方法，通过蒙特卡洛模拟研究发现，传统的理论驱动求解方法实施条件过于严格，缺乏现实可操作性；各种方法驱动的求解方法都暗含一些不太合理的参数假定，因此很容易得出误导性结论；以往学者在实践中常常使用的经验法则不可靠。基于对这些方法进行的批判性反思，本文介绍了一种被称作边界分析的新的求解思路，并为这一求解思路提供了新的拓展方向。

关键词：年龄—时期—世代分析；理论驱动；方法驱动；边界分析

作者简介：许琪（南京大学社会学院副教授）；王金水（南京大学社会学院博士研究生）；吴愈晓（南京大学社会学院教授）

一、导论

社会变迁是社会学研究的一个永恒主题。早在社会学诞生之初，社会学的奠基人，如韦伯、马克思、涂尔干等就对社会变迁问题有过大量著述。在当代，关于社会变迁的研究方法有了长足发展，学者们认识到，研究社会变迁必须同时关注三个与时间相关的效应：年龄效应、时期效应和世代效应世代。（Yang & Land，2013）。年龄效应指的是个体的观念、态度和行为随年龄呈现出的变动趋势，如个体罹患某种疾病的概率随着年龄增长而上升。时期效应指的是在特定时点上发生的重大社会、经济和政治事件对个体的影响，如营养、医疗和卫生条件的改善会提升人们的健康状况。虽然社会科学领域的研究者很早就关注到了年龄效应和时期效应，但人们对世代效应的认识却经历了一个漫长的发展过程。通俗地讲，世代指的是在同一时点经历同一事件的人，如同一年毕业、同一年结婚或同一年参加工作的人都可以称作一个世代。在具体研究中，学者们关注最多的是出生世代，即在同一时点出生的人。

在学术研究中，法国人口学家列克西斯（Wilhelm Lexis）提出的列克西斯图通常被视作世代效应的起源。此后，世代效应在流行病学和社会学等领域引起了众多学者的关注。20世纪50年代，社会学家曼海姆提出了“代”（generation）的概念，这通常被视为世代的同义语（Mannheim，1952）。此后，莱德（Norman B. Ryder）在社会学研究中正式使用世代一词，并对世代效应给出了完整的理论解释。他认为，世代效应缘于年龄与时期之间的交互作用，且这种交互作用会随时间发生变化，一种典型的变动趋势是“贫者越贫，富者越富”，即存在所谓的累积优势或累积劣势原理（Ryder，1965）。在社会学领域，验证这一原理的经典案例是埃尔德（Glen H. Elder）对美国20世纪30年代经济大萧条的研究。在《大萧条的孩子们》一书中，他详细分析了童年时期经历经济萧条对成年后的工作、生活和职业生涯如何产生持续而深远的影响（Elder，1974）。

在充分认识到世代效应的重要性之后，关于社会变迁的学术研究越来越倾向于在数据分析时同时考虑年龄、时期和世代三个因素。但是，由于年龄、时期和世代之间存在完全共线性（年龄="时期-世代），传统统计方法无法分解出三者对因变量的独立影响，由此产生了年龄—时期—世代模型（APC模型）的参数识别问题。为了克服这一难题，学者们提出了多种求解策略。这些策略中有些是理论驱动的，即根据理论对模型参数施加限定。这类求解策略是否有效取决于研究者使用的理论，由于很多时候并不存在非常明确的理论，或者存在多种有争议的理论，使用这类方法的求解结果往往也存在争议。

为了克服理论驱动的模型求解策略在实际应用中的弊端，近20年来诞生了多种使用统计技术求解APC模型的方法（Yang & Land，2006；Yang et al.，2008），我们将之称作方法驱动的模型求解策略。与理论驱动的求解策略不同，这类方法不需要研究者事先对模型参数施加任何限定条件，因此在实践中获得了很多学者的青睐。但是，这类方法并不能从根本上解决APC模型的参数识别问题。奥布莱恩（Robert M. O’Brien）和罗丽莹等学者（O’Brien，2011；Luo，2013；Luo & Hodges，2015，2020a；Luo et al.，2016）的一系列研究发现，这类方法在求解时都对模型参数施加了某种隐含的限制条件，所以在本质上，它们与理论驱动的求解策略并无区别。但存在的问题是，这类方法施加的限制条件大多基于某种通用的统计原则，而通用的原则不可能应对千差万别的现实情境，因此，使用这些方法得到的结论并不可靠。一些模拟研究甚至发现，使用这些方法有可能得到与真实结果完全相反的结论（Bell & Jones，2014；O’Brien，2017）。

由于从方法角度求解APC模型的很多尝试并不成功，近年来的一些研究开始重新回归理论。与早年的理论驱动的求解策略不同，这些新近的研究认为，基于完备的理论来求解APC模型是不现实的，在实际研究中，相对可行的分析策略是使用一些粗糙但可靠的理论来框定年龄、时期和世代效应的变动范围，福斯（Ethan Fosse）和温希普（Christopher Winship）将这种分析策略称为“边界分析”（Fosse & Winship，2019a）。他们通过两个真实的案例证明，使用相对较弱的理论假定就能获得比较准确的年龄、时期和世代效应的变动范围，进而得到可靠且具有实际指导意义的研究结论。我们认为，福斯和温希普提出的边界分析法为求解APC模型提供了一种新的可能，如果将这种方法与传统的理论驱动的求解方法相结合，会拥有更加广阔的应用前景。但遗憾的是，上述国外学者对传统APC分析方法的批判性反思与最新发展都未能引起国内学者的足够关注。

在国内，随着中国社会的快速发展和大规模抽样调查数据的普及，近年来使用APC模型研究中国社会变迁的实证研究不断增多（高海燕等，2022；吴晓刚、李晓光，2021；吴敏、熊鹰，2021；石智雷等，2020；李婷等，2020；范文婷等，2018；田丰，2017；曹惟纯、叶光辉，2014）。这些研究之中虽然不乏精妙的理论假设和模型构建，但就研究方法而言，绝大多数研究使用的仍是方法驱动的模型求解策略，而如前所述，这种求解策略存在重大缺陷。我们发现，虽然很多学者在研究时已经意识到了这种缺陷，但并未采取有针对性的应对措施。一些学者认为，虽然每种方法都有缺陷，但只要同时使用多种方法，且多种方法估计到的结果相近，就可以得到比较稳健的结论。但这一表面上看来可信的经验准则在实践中是否可靠依然有待检验。

鉴于国内学者有使用APC模型研究中国社会变迁的迫切需求，而现有研究又对这一模型的认识存在较大误区，我们认为，有必要对APC模型的求解方法进行回顾与总结，并为未来的研究指明方向。为了实现这一目标，本文将简要回顾APC模型的发展历程，并通过蒙特卡洛模拟（Monte Carlo simulation）检验各种方法的稳健性。在对传统方法进行批判性反思的基础上，我们将介绍福斯和温希普提出的边界分析法，并结合传统理论驱动的APC模型求解策略对这一方法进行拓展。之后，我们将以中国老年人认知能力的变迁为例，演示如何应用拓展后的边界分析法进行实证研究。在论文的最后，我们将对未来如何开展APC分析提供一些方法上的建议，以期使中国学者能够更好地应用APC模型研究中国社会变迁。

二、APC模型及其求解方法

（一）APC模型的参数识别问题

为了更好地理解APC模型的参数识别问题，有必要首先了解该模型的数据结构。假设通过多期横截面调查，我们采集到受访者在历次调查中的年龄、调查年份（时期）和其他信息。我们可以将年龄和调查年份分为间隔相等的多个类别，并通过如表1所示的年龄与时期交叉分类后的表格来描述该数据。表1中的每条斜线对应一个世代，可以证明，如果年龄有I个类别，时期有J个类别，那么世代将包含K="I+J-1个类别。表1展示的是一个I=6、J=5的特殊情形，相应地，表中共有10（K=6+5-1）个世代。

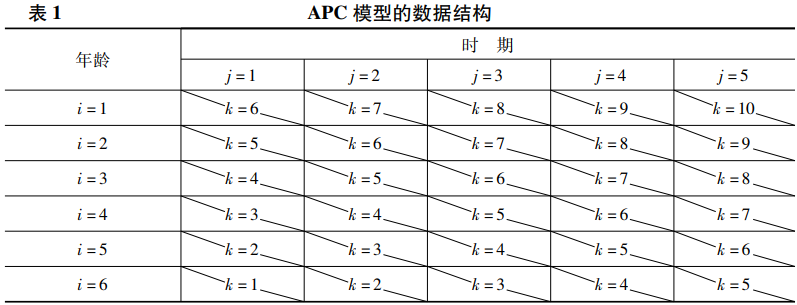
如果用i作为年龄的下标，j作为时期的下标，k作为世代的下标，那么一个因变量Yijk与年龄、时期和世代之间的关系可以通过以下方程来表示：

Yijk="μ+αi+πj+γk+εijk

即便我们按照虚拟变量编码或方差编码的通常做法对模型参数进行常规限定，该模型也是不可识别的。原因在于，该模型包含I+J+K-3个待估参数，但仅包含I+J+K-4个不完全线性相关的自变量。由于年龄="时期-世代，该模型不满秩，常规统计方法无法给出所有参数的唯一解，或者说存在无穷多个解，这些解可以无差别地拟合观测数据。在没有附加信息的情况下，模型无法判断哪个是最优解，这就是APC模型的参数识别存在的问题。

（二）理论驱动的参数识别策略

为了帮助寻找最优解，研究者必须对模型参数施加某种限制条件。梅森（Karen O. Mason）等学者指出，APC模型的秩仅比满秩少1，因此只需对模型参数增加一个额外的限制条件即可求解（Mason et al.，1973）。一个最简单的做法就是将两个参数设为相等，如设置α1="α2、π1="π2或γ1="γ2。该方法不仅适用于因变量是连续变量的线性回归模型，也适用于因变量是二分变量、计数变量或其他变量类型的广义线性模型。因为研究者在应用该方法时必须对待估参数施加一个限制条件，所以，它也被称为受限广义线性回归法（constrained generalized linear regression，下文简称CGLM）。梅森等学者指出，在应用CGLM时，额外增加的限制条件是模型识别的关键，该限制条件必须基于完备的理论。但在实践中，很多时候并不存在这样的理论，或仅存在比较粗糙的理论，基于这样的理论很容易导致模型误设。更加严重的是，一些模拟研究发现，CGLM对限制条件非常敏感，将两个存在细微差异的参数设为相等也会导致极有误导性的结果，所以这一方法在实践中的缺陷很大（Glenn，1976）。

除了CGLM之外，另一种理论驱动的APC模型求解方法是代理变量法或奥布莱恩（O’Brien，2000）所说的特征变量法。该方法的基本思路是寻找年龄、时期和世代的一个代理变量，用以替换被代理的变量求解APC模型。举例来说，如果出生世代的规模是导致世代对因变量产生影响的唯一因素，那么就可以用它替换世代进行APC分析。在实践中，该方法的缺陷是很难找到符合要求的代理变量。正如温希普和哈丁（David J. Harding）所言，该方法要求被代理的年龄、时期和世代变量通过且仅通过一个代理变量对因变量产生影响，这在实践中几乎是不可能做到的（Winship & Harding，2008）。

为了提高代理变量法的可行性，温希普和哈丁提出了一种基于机制分析的APC模型求解方法（Winship & Harding，2008）。该方法允许年龄、时期和世代通过多个中介变量影响因变量，且每个中介变量可以同时作为年龄、时期和世代中多个变量的中介，因而它的假定比代理变量法更弱。但该方法依然要求研究者穷尽年龄、时期和世代中的一个变量对因变量的影响机制，这往往很难实现。正因如此，该方法虽有理论意义，但在实践中很少被应用。

（三）方法驱动的参数识别策略

综上所述，理论驱动的参数识别策略需要研究者做很强的理论假定，这大大限制了它们的应用前景。为了寻找新的求解思路，2000年后，西方学术界兴起了一股使用统计方法求解APC模型的风潮，其中较有影响的是杨洋等学者（Yang et al.，2004；Yang & Land，2006；Yang et al.，2008）提出的内生因子法（intrinsic estimator，下文简称IE）和多层次APC模型求解方法（hierarchical APC model，下文简称HAPC）。下面，我们将概述这两种方法的求解思路与后续研究对这两种方法的反思与批评。

IE在本质上是一种主成分求解法（Luo，2013），它的求解思路是通过主成分分析法把I+J+K-3个自变量构成的向量空间分为两个部分，一是与I+J+K-4个非零特征值对应的非零向量空间（nonnull subspace），二是与零特征值对应的零向量空间（null subspace），然后以非零向量空间中的I+J+K-4个特征向量为自变量拟合回归模型，这样可以得到I+J+K-4个回归系数。但是，与零向量空间对应的特征向量无法同时纳入回归方程，因此，需要人为设置一个回归系数，杨洋等人将之设置为零（Yang et al.，2008）。对此，他们的解释是，零向量空间对因变量没有影响，因此可以将与之对应的系数设为零。但罗丽莹（Luo，2013）的研究却发现，这一设定实际上暗含了一个非常武断的假定，因此，IE的求解结果通常有偏。后续的研究还发现，IE是在所有可能的解中选择了一个参数平方和最小的解，如果用图形展示，这个解在所有可能的解中距离向量空间原点的欧氏距离最短，但距离最短与最优是两个不同的概念（Fosse & Winship，2018）。而且，向量空间中原点的位置取决于自变量的编码方法，例如方差编码与虚拟变量编码的原点就不一样，而且同样是虚拟变量编码，以哪个组作为参照组也会改变原点位置，这导致在不同编码方案下使用IE会得到完全不同的结论（Pelzer et al.，2015；Luo et al.，2016）。正是因为存在这些缺陷，很多学者不建议使用IE来求解APC模型。

除了IE，杨洋和兰德（Kenneth C. Land）还提出了另一种通过多层线性模型求解APC模型参数的方法，即HAPC（Yang & Land，2006，2008）。他们发现，如果将年龄、时期和世代中的一个或两个放到更高层次，使用多层线性模型求解就不会遇到参数识别问题。在实践中，他们建议将年龄作为个人层次的变量，将时期和世代同时作为更高层次的变量来拟合分层交叉随机效应模型。这一方法自提出后得到了广泛的应用，我们关注到，大多数国内学者在使用该方法求解APC模型。这或许是因为多层线性模型已经是一种非常成熟的统计方法，且将时期和世代作为更高层次的变量也比较符合人们的主观感受。但是，后续的很多研究却发现，这种求解方法并不可靠。

罗丽莹和霍奇斯（James S. Hodges）指出，HAPC在求解过程中对模型参数施加了某种隐含假定。他们证明，如果将年龄、时期和世代中的一个设为随机效应，等价于假定该随机效应的线性趋势为零（Luo & Hodges，2020）。如果按照杨洋和兰德的建议，将时期和世代同时设为随机效应，那么在大多数情况下，研究者会得到线性趋势为零的世代效应。这一发现验证了很多模拟研究的结论。例如，贝尔（Andrew Bell）和琼斯（Kelvyn Jones）的多项模拟研究发现，使用HAPC通常会得到无世代效应的结论。他们认为，导致这一结果的主要原因是多层线性模型在求解时需要最小化误差方差，随机效应作为误差的一部分必须服从这一原则（Bell & Jones，2014，2015）。在APC模型中，世代的类别数量往往大于年龄和时期，因而，将世代效应中的线性趋势归入时期或年龄的类别下总能减少误差方差，这导致使用HAPC很容易得到世代效应不存在或没有明显变动趋势的结论，但出现这样的结果不是因为事实就是如此，而是因为使用的方法使然（Bell & Jones，2018）。在实践中，一些研究者试图合并世代效应以减少世代的类别，这样可以减少HAPC的上述缺陷，但合并世代必然会引入参数假定，根据CGLM，合并两个世代意味着假定这两个世代对因变量的影响相同，在使用HAPC时，研究者往往要合并多个世代，这意味着同时施加多个假定，罗丽莹和霍奇斯的模拟研究发现，使用这种方法会得到极有误导性的结论，因此并不推荐（Luo & Hodges，2015）。

值得一提的是，在对杨洋等人提出的IE和HAPC进行猛烈批判之后，罗丽莹和霍奇斯（Luo & Hodges，2022）提出了一种新的APC求解方法：APC交互模型（age-period-cohort interaction model，下文简称APCI）。与以往的求解方法不同，APCI采用了新的APC模型设定方法，如下所示：

Yijk="μ+αi+πj+αiπj+εijk

该模型使用年龄效应αi和时期效应πj之间的交互项αiπj替换了原始的世代效应γk，这也是它被称作APC交互模型的主要原因。罗丽莹和霍奇斯认为，上述新模型有两个明显的优点。首先，该模型中的所有参数均可使用常规方法求解，因此不存在经典APC模型中的参数识别问题。其次，基于交互项αiπj不仅可以算出世代效应γk，而且可以分析世代效应随时期的变动趋势。罗丽莹和霍奇斯（Luo & Hodges，2022）认为，他们提出的新APC模型及求解方法很好地反映了莱德的世代理论。根据这一理论，世代效应缘于年龄与时期之间的交互，且会随时期发生变化（Ryder，1965）。

由于APCI是2020年提出的新方法，目前还没有关于该方法的进一步研究。我们仅在此表达我们对该方法的两点评论。首先，我们同意罗丽莹和霍奇斯提出的该模型不存在参数识别问题的观点，但我们并不认为使用该模型能够得到年龄、时期和世代效应。正如两位作者在文中指出的，他们的新APC模型是一个更加一般化的模型，传统APC模型是新模型的一个特例，因为假定世代效应不随时间变化，该模型就等价于传统APC模型。那么存在的问题是，在对模型参数施加限定后的传统APC模型是不可识别的，那为什么不施加任何限定的更加一般化的新模型反而是可以识别的呢？其次，罗丽莹和霍奇斯认为，他们的模型可以分析世代效应随时间变动的趋势，这一思想很早就有人提出（Mason & Fienberg，1985），但因为缺乏可行性而没有得到关注。这主要是因为传统APC模型已是不可识别的，如果再允许世代效应随时间变化，那么势必增加模型识别的难度。但罗丽莹和霍奇斯却声称，在不需要额外假定的情况下就可做到这一点。考虑到他们的模型确实是一个可以识别的模型，我们认为，唯一可能的解释是该模型识别出的参数不是作者所说的年龄、时期和世代效应的无偏估计值。下面，我们将通过一个模拟研究验证上述观点。

三、对不同方法的蒙特卡洛模拟

为了检验各种模型求解方法的有效性，我们开展了一项蒙特卡洛模拟研究。在进行蒙特卡洛模拟的过程中，研究者需要设定一套总体参数或假定一个数据生成机制（data generating mechanism），与此同时引入随机扰动，通过反复模拟数据并应用某种统计方法，研究者可以观察这种方法能否一致地估计出设定的总体参数值，据此判断该方法是否有效。使用蒙特卡洛模拟的好处是，研究者事先知道参数的真实值，这就为评估方法好坏提供了一个黄金标准。它的缺陷在于，研究者永远无法穷尽参数的所有可能取值，因此，某种方法在设定的参数下表现良好不代表它在其他情况下也能得到合意的结果。不过，一旦某种方法无法在特定参数条件下得到理想的估计值，就可以证伪该方法。

在以往的研究中，已有很多学者使用蒙特卡洛模拟评估各种APC模型求解方法的有效性（Bell & Jones，2014，2015；O’Brien，2011，2017；Luo & Hodges，2015，2020），但这些研究大多仅评估一种方法，少有研究在一次模拟中同时评估多种方法。此外，对于罗丽莹和霍奇斯（Luo & Hodges，2022）最新提出的APCI，学术界尚缺乏可靠的模拟研究来验证。最后，我们也试图通过模拟研究来检验一些国内学者在应用APC模型时常用的经验法则（如多种方法的结果相近可以推断出结论可靠）是否具有现实可行性。

具体来说，我们将年龄设置为6个类别，时期设置为5个类别，因此数据中共包含10个出生世代，与之对应的数据结构如表1所示。我们假定每个年龄与时期的交互组合都包含400名观察个案，因此，总样本量为12000（N="I×J×400=12000）。我们根据如下所示的表达式生成数据：

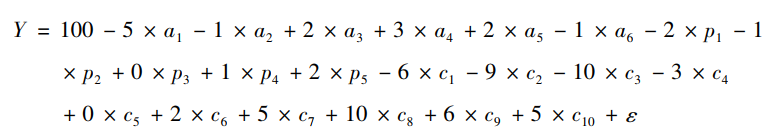
在该表达式中，Y是因变量，a1~a6是与年龄对应的6个虚拟变量，p1-p5是与时期对应的5个虚拟变量，c1~c10是与世代对应的10个虚拟变量，模型的截距为100，各变量对因变量的真实影响如上式所示，模型还包含一个随机误差项ε，我们假定它服从标准正态分布。仔细观察上述表达式可以发现，年龄效应呈先上升后下降的二次曲线变化；时期效应是线性递增的；世代效应大体呈上升趋势，但呈现一定的波动性。我们根据上述表达式生成了1000套数据，并同时使用6种方法对这1000套数据进行APC分析，在将1000次模拟的计算结果取平均值以后，我们得到了如表2所示的结果。

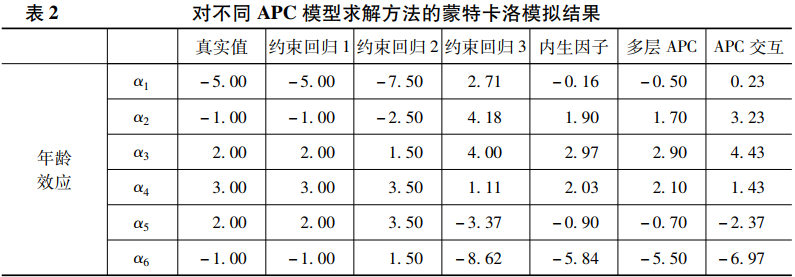
表2中真实值这一列给出了真实的总体参数。与约束回归1~3这三列对应的是三种约束回归法的求解结果。其中，约束回归1采用了完全正确的参数限定条件，具体来说，我们将γ7设置为等于γ10，根据数据生成机制，这两个参数确实相等。从表2可以发现，如果采用这一设定，使用约束回归法可以得到总体参数的无偏估计值。但我们知道，上述理想情况是可遇而不可求的，在具体分析时，研究者很难做出如此精准的设定。比较现实的情况是，研究者只能根据一些粗糙的理论对模型参数进行相对准确的设定。例如，基于某种理论将γ9设置为等于γ10。从表2可知，这已是一个比较准确的设定了，因为γ9与γ10的真实值仅相差1。但是，如此细微的差异却会导致模型估计结果发生重大改变。从约束回归2这一列可以发现，进行上述设定之后，时期效应全部变成了0，因此如果采用这一模型，我们会误以为因变量不随时期发生变化。

除了对模型参数进行局部限定，研究者也可以将年龄、时期和世代效应中的部分类别合并。在实际研究中，最常见做法是合并世代，因为与年龄和时期相比，世代的类别较多。合并世代有多种方法，有时研究者会基于理论将部分世代合并；而在另一些时候，合并可能完全出于某种似是而非的经验法则，例如将所有相邻的两个世代合并。约束回归3给出了基于经验法则将相邻世代合并后的求解结果。可以发现，采用这种方法得到的年龄效应、时期效应和世代效应都存在很大偏差，这主要是因为相邻世代的参数值并不相等，而上述合并方法却假定它们相等。我们关注到，罗丽莹和霍奇斯曾使用蒙特卡洛模拟得到过类似的发现（Luo & Hodges，2015）。总而言之，我们的模拟研究与前人的研究都发现，通过合并相邻类别来打破年龄、时期和世代之间的完全共线性只是研究者的一厢情愿的做法，在实践中，这种方法很难收到好的效果。

除了上述三种CGLM，我们还使用IE、HAPC和APCI这三种通用的模型求解方法对模拟数据进行分析。从表2可以发现，这三种通用方法的求解结果很接近。如果根据多种方法结果一致即可得到可靠结论的经验法则，研究者就很容易下结论，但这个结论是错误的。如果将这三种方法的估计结果与总体真值进行比较，可以发现无论是年龄效应、时期效应还是世代效应都存在较大偏差。以世代效应为例，真实的世代效应虽有波动，但总体呈上升趋势，然而这三种方法得到的世代效应都没有呈现明显的上升趋势。我们的上述模拟研究验证了以往对HAPC的基本结论，也即使用该方法无法得到有明显趋势的世代效应（Bell & Jones，2018）。不仅如此，我们也对罗丽莹和霍奇斯最新提出的APCI进行了检验，我们发现，这个方法也不能得到年龄效应、时期效应和世代效应的合理估计值，至少在我们模拟的这套参数下不能。

四、边界分析及其拓展

上述研究充分表明，传统的理论驱动的APC模型求解策略和方法驱动的APC模型求解策略都存在重大缺陷。为了克服这种缺陷，福斯和温希普提出了一种被称作边界分析的新方法（Fosse & Winship，2019b）。他们认为，以往关于APC模型的求解方法都试图得到年龄、时期和世代效应的点估计值，在缺乏可靠理论支撑的情况下，这个目标很难实现。一个退而求其次的目标是估计这三个效应的合理区间或边界。下面，我们将简要介绍边界分析法的原理，并讨论如何结合传统的理论驱动的模型求解策略对之加以拓展。

（一）不可识别模型中的可识别参数

如前所述，APC模型是不可识别的，但这并不意味着该模型的所有参数都是不可识别的。福斯和温希普证明，真正不可识别的是年龄、时期和世代效应的线性趋势，而这三个变量对因变量的非线性影响是可以求解的（Fosse & Winship，2019b）。为了说明这一点，我们可以把年龄、时期和世代效应分解为相互独立的两个部分：一是这三个变量对因变量的线性影响，二是它们对因变量的非线性影响。以年龄效应为例，我们可以将之表示为：

上式中，i为年龄效应的下标，i*为i的均值，它可以通过公式i*="(I+1)/2得到。i-i*等价于对i进行中心化处理，其回归系数α刻画了年龄对因变量的线性影响，而i代表的是排除线性趋势之后因变量随年龄的非线性波动。按照同样的方法，我们可以将时期效应πj和世代效应γk也分解为相互独立的线性部分与非线性部分。将它们同时代入APC模型就可得到如下表达式：

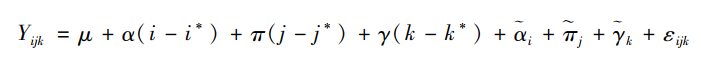
福斯和温希普将之称为线性化后的APC模型（linearized APC model）。可以证明，上述线性化后的APC模型与传统APC模型完全等价，但与传统模型相比，新模型有两个明显的优势。首先，福斯和温希普证明，该模型中的参数i、j和k存在唯一解，但α、π和γ不存在唯一解。所以，APC模型的参数识别问题仅针对年龄、时期和世代效应的线性部分，而不针对其非线性部分。其次，福斯和温希普进一步证明，虽然α、π和γ不存在唯一解，但三者的特定组合却可以求解（Fosse & Winship，2019b）。具体来说，因为(j-j*)="(k-k*)+(i-i*)，将之代入线性化后的APC模型，可以得到以下表达式

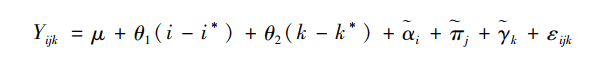
可以证明，θ1和θ2存在唯一解。

综上所述，虽然APC模型作为整体不可识别，但年龄、时期和世代效应的非线性趋势与三者线性趋势的特定组合却存在唯一解，这在实践中具有非常重要的意义。首先，年龄、时期和世代效应的非线性趋势本身就有一定的研究价值。其次，仅得到三者线性趋势的特定组合也可以在一定程度上判断因变量随年龄、时期和世代的线性变化。举例来说，如果θ1大于零，则意味着年龄和时期的线性趋势不能同时为负。如果θ1等于0，则有两种可能性，一是年龄和时期的线性趋势同时为0，二是这两个变量的线性趋势一正一负，且在数值上大体相等。总之，通过求解APC模型中的可识别参数，我们已经可以对年龄、时期和世代效应做出大致的判断，但仅有这些还是不够的，接下来要做的就是基于可靠的理论进一步缩小年龄、时期和世代效应的取值范围。

（二）框定年龄、时期和世代效应的边界

福斯和温希普认为，要进一步缩小年龄、时期和世代效应的取值范围，研究者可以采用两种策略（Fosse & Winship，2019b）。

一是基于理论对α、π和γ的符号进行限定。举例来说，假设某种理论认为因变量随年龄呈上升趋势，基于此可以得到α>0。因为α+π="θ1，且θ1可以直接求解得到，据此可以推论出π<θ1。除此之外，因为π+γ="θ2，且θ2可以直接求解得到，据此可以推论出γ>θ2-θ1。

二是对αi、πj和γk的形状进行限定，这种限定需同时考虑年龄、时期和世代效应的线性部分与非线性部分。举例来说，假设根据某种理论，可以推断出因变量随年龄单调下降，这意味着将年龄效应的线性部分与非线性部分相加后得到的总效应将随年龄的增长呈单调下降趋势。据此，可以得到α的最大值，假设为-2。在得到α<-2的限定条件之后，再结合θ1与θ2的取值，就可以对π和γ的取值范围进行限定。在本例中，π>θ1+2，γ<θ2-θ1-2。

（三）对边界分析法的蒙特卡洛模拟

接下来将使用与上文相同的数据对边界分析法进行蒙特卡洛模拟。在将1000次模拟结果取平均值以后，我们得到了如表3所示的结果。该表第三列给出了年龄、时期和世代效应的非线性趋势的估计值。此外，我们还可求得θ1="1.86，θ2="3.42。这意味着年龄与时期效应的线性趋势之和（α+π）为1.86，而时期和世代效应的线性趋势之和（π+γ）为3.42。接下来我们要做的就是进一步框定这三个线性趋势的取值范围。

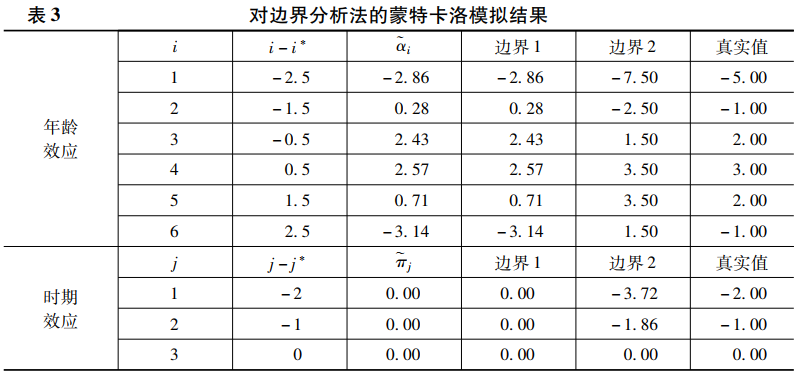
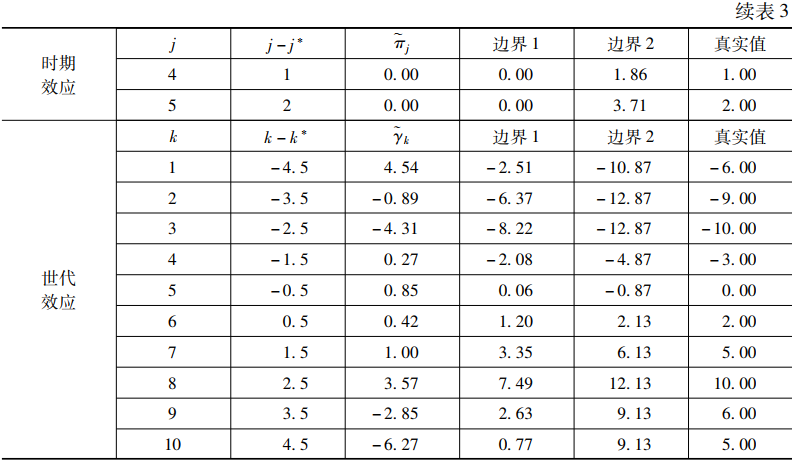
首先，如果根据某理论能有较大的把握认为年龄效应的线性趋势α>0，那么我们就能据此缩小π和γ的取值范围。因为α>0，且α+π="1.86，这意味着π<1.86。此外，因为π<1.86，且π+γ=3.42，这意味着γ>1.56。这样，我们就得到了α、π和γ的第一组限定条件，即α>0，π<1.86，γ>1.56。

其次，如果进一步假定时期效应的线性趋势π>0，那么就可以按照与之前类似的方法缩小α和γ的取值范围。具体来说，因为π>0，且α+π="1.86，这意味着α<1.86。此外，因为π>0，且π+γ=3.42，这意味着γ<3.42。这样就得到了α、π和γ的第二组限定条件，即α<1.86，π>0，γ<3.42。

最后，将α、π和γ的两组限定条件结合起来，就得到了α、π和γ的最终取值范围，即0<α<1.86，0<π<1.86，1.56<γ<3.42。将之代入αi、πj和γk的计算公式，就能得到表3中的边界1和边界2。表3的最后一列给出了αi、πj和γk的真实值，可以发现，真实值恰好处于这两个边界之间。因此，只要能对α、π和γ的取值符号进行正确设定，就能使用边界分析法得到年龄、时期和世代效应的正确取值范围。如果还能对αi、πj和γk的形状施加某种限定，就能进一步缩小区间的估计范围，因而，边界分析法也将变得更加有效。

（四）拓展边界分析

综上所述，福斯和温希普提出的边界分析法为求解APC模型提供了新思路，但这种方法在实践中也会遇到估计区间过宽的问题。以上文的蒙特卡洛模拟为例，估计得到的α值在0~1.86，虽然α的真实值1落在这个区间范围内，但如此之大的波动范围使得研究者难以对时期效应的真实大小做出精确的判断。如果我们能直接对α、π和γ的取值大小进行限制，而不仅仅是对其取值方向进行限制，就能进一步缩小它们的取值范围。我们关注到，福斯和温希普在文中确实提到了这种限定策略。例如，根据某理论直接假定α>1。但这样的限定过于武断，几乎没有理论能提供合理的参考值，因此他们并未对该方法进行论述。但我们认为，这种限定策略并非完全不可能。

上文提到，温希普和哈丁（Winship & Harding，2008）曾经提出过一种基于机制分析的APC模型求解方法。使用该方法需要穷尽年龄、时期和世代中至少一个变量对因变量的因果机制，这在实践中很难实现，因此并未得到广泛应用。我们认为，若要穷尽所有因果机制确实很难，但寻找一个或少数几个因果机制却不难做到。温希普和哈丁认为，如果研究者只能找到部分因果机制，那么APC模型只能得到部分识别。从获得点估计的角度来说，部分识别是没有用的，因为部分识别的结果是有偏差的；但从区间估计的角度来说，部分识别的模型却有很大用途。举例来说，如果能找到年龄的一个中介变量X1，那么运用温希普和哈丁的方法，可以很容易求得年龄经由X1对因变量的线性影响αX1，假设αX1>0。如果年龄经由其他中介变量对因变量的线性影响与αX1具有相同的影响方向，那么可以推断出α>αX1，这样就能直接对α的取值找到一个合理的下限。下面，我们通过一个案例进行演示。

五、经验示例

（一）数据与变量

我们以中国老年人认知能力的变迁为例，演示如何应用拓展后的边界分析法开展实证研究。具体使用的数据来自2002—2014年“中国老年健康影响因素跟踪调查”（以下简称CLHLS）。该调查于1998年正式启动，此后在2000年、2002年、2005年、2008年、2011年、2014年先后进行了六次跟踪调查。1998年和2000年的调查样本主要针对80岁以上的高龄老人，在2002年后，CLHLS将样本的年龄范围扩大到了65岁及以上。为了使样本的年龄范围具有可比性，我们仅使用2002年以后开展的五次调查数据进行研究。

具体研究时，我们删除了历次调查中年龄在100岁以上的老年人，在进一步删除缺失值以后，实际使用的样本量为55838人。考虑到CLHLS对高龄老人进行了过额抽样，我们使用了数据提供的权重对分析结果加权。分析使用的变量包括老年人的认知能力得分、年龄、调查时期、世代和教育年限。因为时期的跨度为3年，我们将年龄也分为3岁一组，这样得到12个年龄组。然后，基于12个年龄组和5个时期得到16个世代。最后，考虑到教育对认知能力有重要影响，且总体而言，中国人的教育程度随世代呈上升趋势，因此，我们认为教育是世代效应得以产生的一个重要机制。

（二）统计方法求解结果

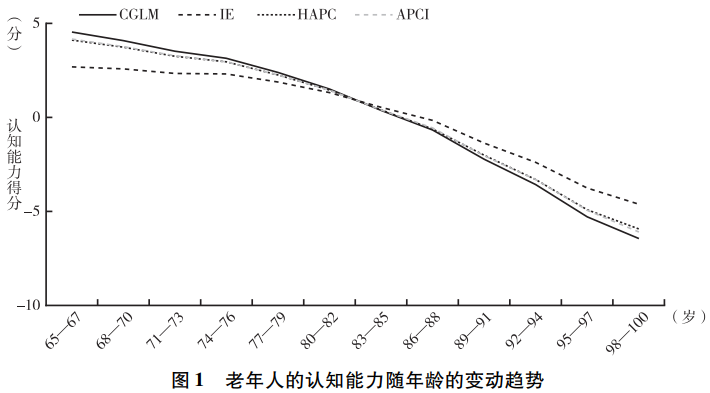
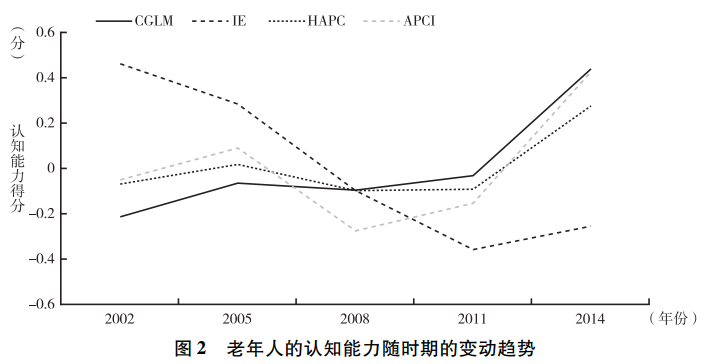
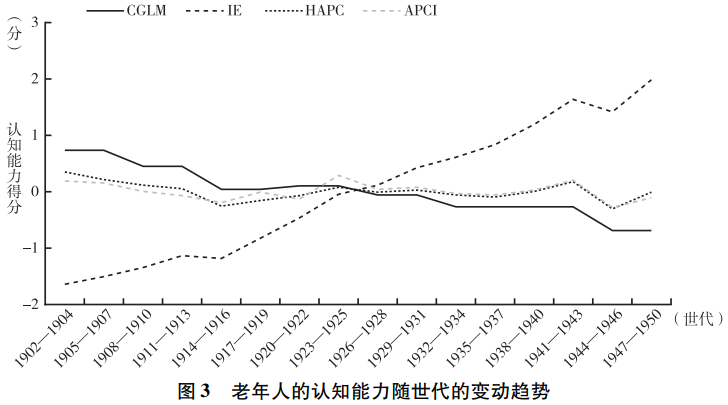
在使用边界分析法之前，我们首先使用CGLM、IE、HAPC和APCI这四种方法研究了老年人的认知能力随年龄、时期和世代的变动趋势，结果见图1~图3。在使用CGLM法时，我们采用了将相邻两个世代合并的方法。分析结果显示，老年人的认知能力随年龄呈明显的下降趋势，且无论采用何种方法，该结论都不变。但在时期效应和世代效应两个方面，不同方法得到的估计结果却不相同。总体来看，HAPC和APCI的估计结果非常接近，这两种方法均发现世代效应几乎为0，而时期效应则围绕0呈不规则波动。CGLM的分析结果与这两种方法也比较接近，该方法发现，世代效应呈微弱的下降趋势，而时期效应则表现出一定的上升趋势。相比之下，IE的估计结果与其他方法存在较为明显的差异，该方法发现时期效应不断下降，而世代效应则不断上升。

面对这些不同的估计结果，我们该如何选择呢？根据以往通常使用的经验法则，研究者很可能率先排除IE，因为该方法的估计结果与其他三种方法存在非常明显的差异。一些研究者可能还会排除CGLM，因为该方法与HAPC和APCI也存在一些差异，且通过该方法发现的认知能力一代不如一代的结论也与直观感受不符。最终，胜出的模型很可能是HAPC和APCI。这两种方法都发现，认知能力存在明显的年龄效应，但不存在世代效应和时期效应。这等于认为老年人认知能力的衰退是一种自然的生理现象，与社会经济的发展无关。但显然这一结论与我们的日常观察并不相符。一方面，随着教育的普及和扩张，中国老年人的教育程度随世代呈明显的上升趋势，这很可能对年轻世代的认知能力产生积极影响。另一方面，年轻世代相比年长世代拥有更加丰富的物质生活和精神文化生活，且中国快速的经济社会发展很可能对年轻世代的认知能力产生更大的提升作用。因此，我们预期在认知能力方面会出现一代更比一代强的结果，但HAPC和APCI却共同发现，中国老年人的认知能力不随出生世代发生变化，这很难得到合理解释。

（三）边界分析结果

其次，我们还可以基于理论对γ的取值进行限定。如前所述，教育扩张和快速的社会经济发展很可能对年轻世代的认知能力有更大的提升作用，因此我们预期γ>0。接下来，我们可以效仿之前对年龄效应的限定方法，进一步假定世代的总效应γi单调递增，但这是一个很强的假定。与年龄不同，世代不是一个连续变量，假定世代的总效应单调递增很可能会对一些特殊世代产生错误的估计。在这项研究中，如果假定世代的总效应单调递增，会得到γ>0.481，这就与上面得到的γ<0.303产生了矛盾。因此，一个更加合理的假定是，世代的总效应在波动中上升。这个假定虽然更加合理，但据此我们只能假定γ>0。在没有其他信息的情况下，我们无法进一步缩小γ的取值范围。

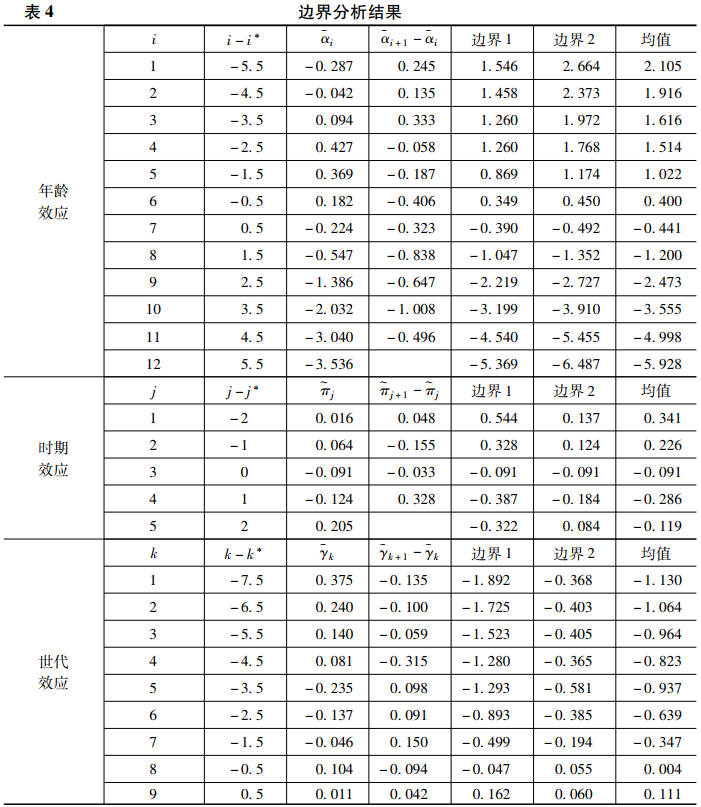
为了获得更加准确的γ的取值范围，我们可以使用温希普和哈丁提出的机制分析法。具体来说，我们认为教育扩张是导致世代效应总体呈上升趋势的一个重要机制，但考虑到世代还会通过其他途径对认知能力产生影响，因此，通过教育这个中介变量我们可以估计出世代效应的下限。参照温希普和哈丁的建议，我们可以通过三步法来计算这个下限。第一步：以认知能力为因变量，教育年限为自变量拟合回归模型，同时控制世代的非线性效应，通过该模型得到的教育年限的回归系数为0.250。第二步：以教育年限为因变量、世代的线性部分（i-i*）为自变量拟合回归模型，分析时同样控制住世代的非线性影响，通过该模型得到的世代对教育年限的线性影响为0.397。第三步：将前两步得到的回归系数相乘，得到世代经由教育年限对认知能力的线性影响为0.099，它就是γ的下限。然后，结合θ1与θ2的取值，我们还可以进一步得到在γ>0.099的情况下，α>-0.537，π<-0.060，如果将α、π和γ的这三个临界值代入原方程中，就可以得到表4中的边界2。

表4最后一列给出了边界1和边界2的均值，这可以视作点估计的一个参考值（Fosse & Winship，2019b）。从中可以发现，年龄效应和时期效应大体呈下降趋势，而世代效应则在波动中上升。如果将边界分析的结果与之前使用各种统计方法得到的结果进行比较，可以发现只有IE与之比较接近。但如前所述，IE反而是最可能被研究者排除的答案，因为它的分析结果与其他几种方法存在非常明显的差异。这里，我们并不是说IE比其他方法更可能得到真实值，因为没有一种统计方法可以保证在任何情况下都比其他方法更可能得到真实值，我们进行这种比较的目的是想证明，以往研究经常使用的经验法则（如一致的估计结果可能更正确）在实践中是行不通的。如果研究者一定要在多种统计分析结果中进行筛选，上文提出的边界分析法可以提供更加可靠的筛选标准。

六、结论与讨论

APC模型是研究社会变迁的一个重要方法和工具，但因为年龄、时期和世代之间存在完全共线性，求解该模型一直被认为是一个难以完成的任务。近半个世纪以来，国外学者或者从理论出发，或者从方法出发，提出了多种求解该模型的思路或策略。理论驱动的求解思路或策略需要研究者做很强的理论假定，因而只在理论上可行，在实践中的应用前景不大。方法驱动的模型求解策略都暗含一些很难验证的参数假定，这些假定往往与实际情况相差甚远，所以使用这类方法也很容易得出有误导性的结论。本文通过一项蒙特卡洛模拟研究验证了上述观点。除此之外，我们通过模拟还发现，以往学者在实践中常常使用的一些经验法则并不可靠。例如，将相邻世代合并不能得到合意的结果，即便多种方法的估计结果一致也不能说明得到了可靠的研究结论。

综上所述，APC模型并不存在一个通用的求解方法，这似乎已成为近年来国外学者的一个共识。但遗憾的是，国内关于APC模型的应用研究仍在大量使用IE、HAPC等统计求解方法，一些学者甚至误以为，使用这些方法无需对模型参数设置任何假定。实际上，正如本文所指出的，所有APC模型求解方法都有假定，只不过有些方法需要研究者人为设置假定，而有些方法则是内在地为研究者设置好了假定。理解每种方法背后的假定非常重要。因此，研究者无论是使用传统的理论驱动的求解方法还是IE、HAPC等通用的求解方法，都应在应用前对每种方法背后的假定条件进行理论论证。如果研究者无法为传统的APC求解方法提供完备的理论支撑，那么福斯和温希普提出的边界分析法就不失为一个可行的替代方案。这个方法的最大优势是只需通过一些比较粗糙的理论就可大致框定年龄、时期和世代效应的取值范围。我们认为，从估计精度的角度来说，点估计总比区间估计来得精确，因此，如果能基于完备理论求得点估计当然更好。但是，如果区间估计足够狭窄，那么从实用性的角度来说就与点估计没有太大差别。在实践中，研究者可以使用福斯和温希普提出的符号限定策略与形状限定策略缩小待估参数的取值范围，也可使用本文提出的基于因果机制的限定策略直接对参数的取值大小进行限定。不过尽管如此，研究者得到的参数取值区间可能依然很宽，这是边界分析法的一个缺陷。除此之外，使用边界分析法必须要借助理论，虽然这个理论不需要像传统的求解方法所要求的那样完备，但对于一些探索性研究，相关理论比较匮乏，这时就无法使用该方法。最后，本文提出的拓展后的边界分析法需要借助额外的中介变量来估计取值区间，如果数据中缺少这些变量，该方法也无法使用。

综上所述，APC模型仍是一个在发展中的方法，目前提出的所有求解方法都有优势，也都有缺陷。不过就目前的发展态势来看，理论在APC研究中的重要性正在逐步增强，这主要体现在以下两个方面。

一是在求解过程中，如果能找到足够有说服力的理论，就可以基于该理论大大提高APC分析的可信度。我们认为，求解APC模型所需的理论必须要与具体的国情和研究问题相结合，中国的很多问题与国外不同，因此不宜照搬国外的研究。国内很多研究实际上是在复制国外的同类研究，例如国外学者使用A方法研究某问题，国内学者也会同样使用A方法研究该问题。这样做有时候是可以的，但有时候也会出现问题。因为中国的国情与国外不同，在国外使用A方法能满足模型背后的假定，但在中国这个假定可能会被违反。因此，在做APC分析时，研究者需要充分论证模型背后的假定是否与实际情况相符，然后才能找到恰当的分析方法。

二是在解释过程中，我们认为，学术界对APC模型的使用不应仅停留在求解层面，而应更进一步，对年龄、时期和世代效应得以发生作用的机制给予可信的理论解释。年龄、时期和世代效应只是一种表层表象，在表层背后掩藏着错综复杂的因果关系。如果不能对年龄、时期和世代如何对因变量产生影响的机制做出深入的理论分析和解释，APC分析就无法为社会科学研究者认识社会变迁提供足够的帮助。从这个角度来说，福斯和温希普的边界分析法只是社会科学家重新将理论引入APC分析的一个起点，未来在如何结合理论来求解和解释APC模型方面还有很长的路要走。

（注释与参考文献从略，全文详见《社会学研究》2022年第6期）